Zestaw obrazów 2019
zdjecie1.jpg
zdjecie2.jpg
zdjecie3.jpg
zdjecie4.jpg
zdjecie5.jpg
zdjecie6.jpg
2019_1.JPG
2019_2.JPG
2019_4.JPG
Events Calendar
Link do spotkania w aplikacji Microsoft Teams: https://tiny.pl/371sncn3
Abstract
Non-Maxwellian Plasma Dispersion Function Evaluation Supported by Rational Approximation and Riemann-Zeta Function
Adrian Drzazga, M.Sc., Application Engineer, Tespol Engineering
The Plasma Dispersion Function (PDF) evaluation is still an important and well-posed problem in modern plasma physics, especially for the Thomson scattering.
We would like to propose the Rational Approximation Method supported by the Riemann-Zeta Function (RFZ) Tools (mostly the RZF itself and analytical tools taken from analytic number theory) to improve the PDF evaluation having the following generalization based on the multipole denominator as provided recently by Skolar [1]:
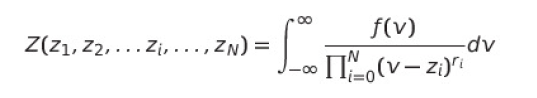
It is well known as the GPDF with an arbitrary number „N” of poles of order „r” and the distribution function f(v) for the non-Maxwellian case.
The topic will be proposed as a conjecture for the problem related to the GPDF (to be presented in PART I: PRELIMINARY RESULTS). We are going to present an analytical and numerical tools to investigate the dispersion function having multipoles using a new approach coming from cross-domains: rational functions, analysis of several complex variables and analytic number theory related to the Riemann-Zeta function and its twin versions.
References
- Skolar, Chirag R., William J. Longley, and Lindsay V. Goodwin. "Computing the generalized plasma dispersion function for non-Maxwellian plasmas, with applications to Thomson scattering." arXiv preprint arXiv:2502.01811 (2025).
- Huasheng Xie; Rapid computation of the plasma dispersion function: Rational and multi-pole approximation, and improved accuracy. AIP Advances 1 July 2024; 14 (7): 075007. https://doi.org/10.1063/5.0216433
- B. C. Foo, D. B. Schaeffer, P. V. Heuer; Recovering non-Maxwellian particle velocity distribution functions from collective Thomson-scattered spectra. AIP Advances 1 November 2023; 13 (11): 115328. https://doi.org/10.1063/5.0169393
- Stucchi R, Lauber P. Landau damping for non-Maxwellian distribution functions. Journal of Plasma Physics. 2025;91(2):E44. doi:10.1017/S0022377825000108
- Milder, A. L., Ivancic, S. T., Palastro, J. P., and Froula, D. H. Impact of non-Maxwellian electron velocity distribution functions on inferred plasma parameters in collective Thomson scattering. United States: N. p., 2019. Web. doi:10.1063/1.5085664.
- Katz, Nicholas, and Peter Sarnak. "Zeroes of zeta functions and symmetry." Bulletin of the American Mathematical Society 36.1 (1999): 1-26.
- A. Semlyen and B. Gustavsen, "Vector fitting by pole relocation for the state equation approximation of nonrational transfer matrices", Circuits Systems Signal Process, vol. 19, no. 6, pp. 549-566, 2000.
Research projects carried out at the IPPLM are funded by the Polish Ministry of Education and Science, the National Science Centre and by the European Commission within the framework of EUROfusion Consortium under grant agreement No 101052200. Financial support comes also from the International Atomic Energy Agency, European Space Agency and LaserLab Consortium as well as from the Fusion for Energy Agency.


















